문제
https://www.acmicpc.net/problem/11049
11049번: 행렬 곱셈 순서
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같
www.acmicpc.net
사용한 알고리즘
2022.01.19 - [PS/Algorithm] - [알고리즘 개념정리] 3. 동적계획법(DP)
문제 이해
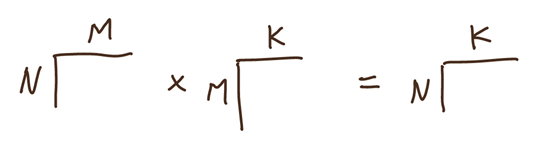
크기가 N×M인 행렬, 크기가 M×K인 행렬을 곱하면 크기가 N×K인 행렬이 되고
총 N×M×K번의 곱셈 연산이 필요하다.
행렬 여러 개를 곱할 때 필요한 곱셈 연산의 횟수는 행렬을 곱하는 순서에 따라 달라진다.

행렬의 곱 ABC를 구하는 경우를 생각해보자.

AB를 먼저 곱하고 C를 곱하는 경우
(AB)C에 필요한 곱셈 연산의 수는 5×3×2 + 5×2×6 = 30 + 60 = 90번이다.

BC를 먼저 곱하고 A를 곱하는 경우
A(BC)에 필요한 곱셈 연산의 수는 3×2×6 + 5×3×6 = 36 + 90 = 126번이다.
같은 곱셈이지만, 곱셈을 하는 순서에 따라서 곱셈 연산의 수가 달라진다.
따라서 이 문제에서 구하고자 하는 값은
행렬 N개의 크기가 주어졌을 때, 모든 행렬을 곱하는데 필요한 곱셈 연산 횟수의 최솟값이다.
풀이
마지막 상황에는 덩어리 2개를 곱해야 한다.
그리고 그 덩어리 2개도 각각 어떠한 덩어리 2개를 곱해서 만들어졌다.
따라서 점화식을 다음과 같이 설정할 수 있다.
dp[L][R] = dp[L][K] + dp[K+1][R] + {mat[L][0] * mat[K][1] * mat[R][1]} (L<K<R)
dp[L][R]은 L번째 행렬에서 R번째 행렬까지 곱했을 때 나오는 최소 곱셈 횟수이고,
mat[K][0]과 mat[K][1]은 각각 K번째 행렬의 행과 열의 개수이다.
기저 조건은 dp[X][X]=0이다.
예를 들어보자.

이 행렬들을 곱할 때 K를 B라고 하면,
dp[A][C] = dp[A][B] + dp[C][C] + {mat[A][0] * mat[B][1] * mat[C][1]} 이다.
시간 복잡도
서로 다른 (L, R) 쌍의 개수는 O(N^2) 개이고,
한 부분 문제를 풀 때 필요한 반복문의 수행 횟수는 O(R-L)번 (최대 N번)이다.
따라서 총 시간 복잡도는 O(N^3)이다.
소스코드
#include <iostream>
using namespace std;
/*
dp[L][R]은 L번째 행렬에서 R번째 행렬까지 곱했을 때 나오는 최소 곱셈 횟수이고,
mat[K][0]과 mat[K][1]은 각각 K번째 행렬의 행과 열의 개수이다.
*/
int dp[501][501], mat[501][2];
int n;
int solve(int L, int R){
if(L==R) // 기저 조건은 dp[X][X]=0이다.
return 0;
else if(dp[L][R]) return dp[L][R]; // 한 번 계산한 값은 저장해뒀다가 재활용(메모이제이션)
else {
dp[L][R]=2147483647;
// K값에 따라 dp[L][R]이 달라지는데, 그중 최소값을 dp[L][R]에 담아준다.
for(int K=L; K<R; K++){
dp[L][R]=min(dp[L][R],solve(L,K)+solve(K+1,R)+mat[L][0]*mat[K][1]*mat[R][1]);
}
return dp[L][R];
}
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=0; i<n; i++){
cin>>mat[i][0]>>mat[i][1];
}
cout<<solve(0,n-1);
return 0;
}
참고자료 : https://t-anb.tistory.com/10
'PS > Baekjoon' 카테고리의 다른 글
| [백준/C++] 9251번: LCS(G5) (0) | 2022.01.21 |
|---|---|
| [백준/C++] 9177번: 단어 섞기(G4) (0) | 2022.01.21 |
| [백준/C++] 11055번: 가장 큰 증가하는 부분 수열(S2) (0) | 2022.01.19 |
| [백준/C++] 11053번: 가장 긴 증가하는 부분 수열(S2) (0) | 2022.01.19 |
| [백준/C++] 1932번: 정수 삼각형(S1) (0) | 2022.01.19 |




댓글