Lec 9. Multiplication / Floating Point (Arithmetic for Computers)
- Multiplication
: Multiplicand 피승수 (n-bit) * Multiplier 승수 (m-bit) = Product 결과 (최대 n+m bit)

1) 승수가 1이면 피승수(=피승수*1)을 적절한 공간에 복사한다.
2) 승수가 0이면 0(=피승수*0)을 적절한 공간에 놓는다.
- Multiply in MIPS
: 32bit * 32bit -> up to 64bit

mult $r, $s
: multiply $r and $s, and put the result to HI ans LO
(HI and LO : 특별 레지스터)
mfhi $d (move from hi register)
: move the multiplication result in the HI register to $d
mflo $d (move from lo register)
: move the multiplication result in the LO register to $d
- Multiplication
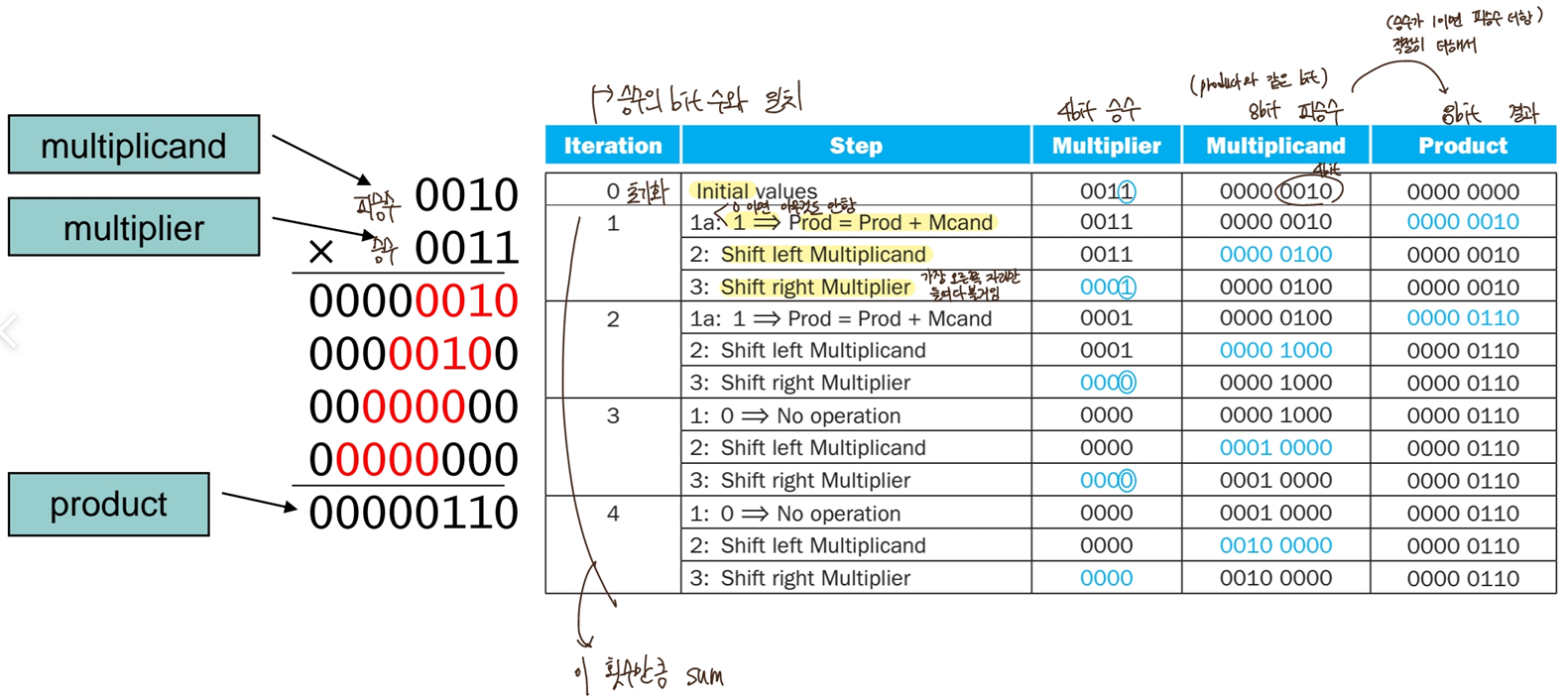
: iteration이 0일때, 승수와 피승수 4bit를 초기화, 나머지는 0으로 초기화.
실질적인 피승수 값은 4bit에 들어있지만 Multiplicand는 Product와 같은 크기인 8bit를 확보해줌.
승수의 bit수 만큼 아래의 두 단계 iteration을 반복함.
->승수가 1이면 Product에 Multiplicand를 더하고 0이면 아무것도 안함.
->그 후, Multiplicand를 Shift left(위치 맞추기), Multiflier를 Shift right(가장 오른쪽 자리의 수만 들여다봄) 해줌.
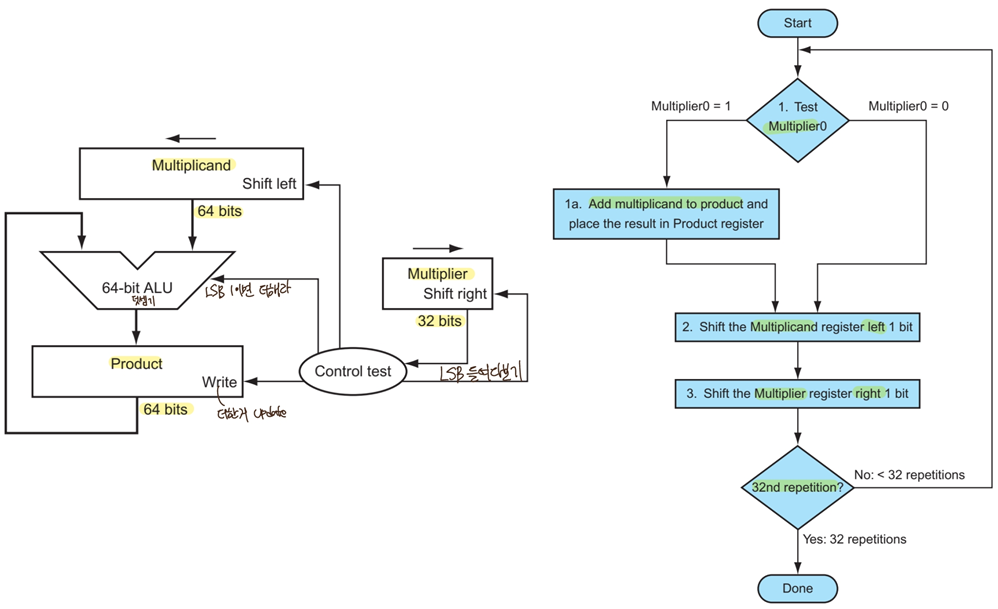
- Floating Point
Normalized
: 10진수에서는 절댓값 기준 1<=x<10 이어야 정규화 되었다고 함,
2진수에서는 절댓값 기준 1<=x<2 이어야 정규화 되었다고 함.
- Floating Point Standard
: IEEE std 754를 기준으로 부동소수점 표현함.
표현법 두가지
-> Single precision (32-bit) : 수업에선 이것만 다룸.
-> Double precision (64-bit) : 더 정밀함.
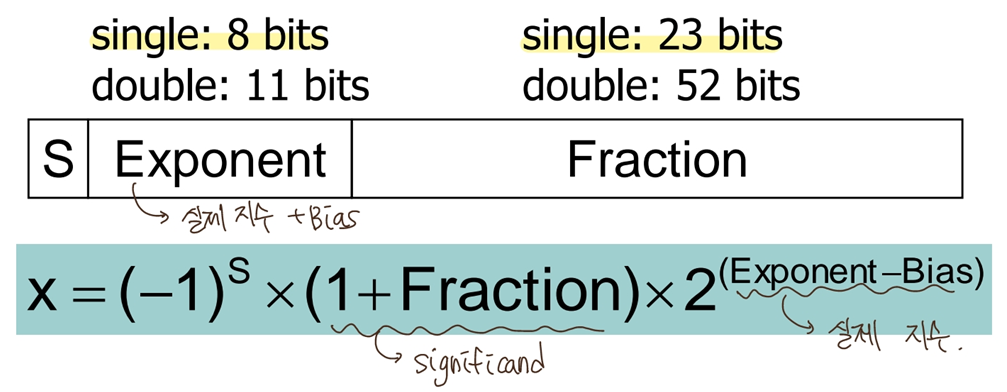
S : sign bit (1이면 negative, 0이면 non-negative)
Normalize significand : 1.0 <= |significand| < 2.0
무조건 1.xx 이므로 1.은 표현할 필요 없음. 그래서 Fraction에 소숫점 뒷자리만 나타냄.
Exponent : actual exponent + Bias (무조건 unsigned 취급)
single precision 에서는 Bias = 127
- Single-Precision Range
: Exponents 00000000 and 11111111 reserved (예약되어있음)
Smallest value (절댓값 기준)
-> Exponent : 00000001
actual exponent = 1 - 127 = -126 (이거보다 작으면 underflow)
-> Fraction : 000..00
significand = 1.0
=> +- 1.0 * 2^-126 ≈ +- 1.2 * 10^-38
Largest value (절댓값 기준)
-> Exponent : 11111110
actual exponent = 254 - 127 = +127 (이거보다 크면 overflow)
-> Fraction : 111..11
significand ≈ 2.0
=> +- 2.0 * 2^+127 ≈ +- 3.4 * 10^+38
ex1) represent -0.75 (10진수)
-0.75 = -1.5 * 2^-1 = -3 * 2^-2 = -11 (2진수) * 2^-2
= (-1)^1 * 1.1 * 2^-1
-> S = 1
-> Fraction = 1000..0
-> Exponent = -1 + 127 = 126 = 01111110
=> 1 01111110 1000...00
ex2) what number is repesented 1 10000001 01000...00
-> S = 1
-> Fraction = 01000...00
-> Exponent = 10000001 = 129
x = (-1)^1 * 1.01 * 2^(129-127)
이때, 1.01 = 1*2^0 + 0*2^-1 + 1*2^-2 = 1.25 이므로
= (-1) * 1.25 * 2^2
= -5.0
- Floating-Point Addition
1) Align binary points
2) Add significands
3) Normalize result & check for over/underflow
4) Round(반올림) and renormalize if necessary(반올림했는데 첫번째 수 건드린 경우)
ex) 4-digit binary example
: 1.000 * 2^-1 + -1.110 * 2^-2 (0.5+ -0.4375)
1) 1.000 * 2^-1 + -0.111 * 2^-1
2) 1.000 * 2^-1 + -0.111 * 2^-1 = 0.001 * 2^-1
3) 1.000 * 2^-4, with no over/underflow
4) 1.000 * 2^-4 (no change) = 0.0625
- FP Adder Hardware
: Floating Point 덧셈은 Integer 덧셈보다 느림,
근데 one clock cycle 에 실수 덧셈 수행하려면 너무 느려짐. 정수 덧셈까지 느려짐. 다른 명령어 전체적으로 느려짐.
(가장 느린 명령어 기준으로 clock 주파수가 낮춰지기 때문)
따라서 실수 산술연산시 파이프라인 사용해서 여러 사이클에 걸쳐 계산하는 것이 좋음.
'CS > 3-1 컴구' 카테고리의 다른 글
| [컴퓨터구조] #11. Single-Cycle MIPS(2) (2) | 2022.04.23 |
|---|---|
| [컴퓨터구조] #10. Single-Cycle MIPS(1) (2) | 2022.04.13 |
| [컴퓨터구조] #8. Performance (0) | 2022.04.01 |
| [컴퓨터구조] #7. MIPS 명령어(7) (0) | 2022.03.31 |
| [컴퓨터구조] #6. MIPS 명령어(6) (10) | 2022.03.26 |




댓글