본문 바로가기
PS/Algorithm

[알고리즘 개념정리] 10. 최단경로 알고리즘

by 이지이즤 2022. 2. 14.
728x90

**본 포스팅은 22Winter 신촌캠프 초급반 강사 dart님의 강의를 참고하여 작성하였습니다.**

 

 

가중치 그래프 

  • 그래프에 더 많은 정보를 표현하기 위해 간선에 여러 가지 속성을 부여할 수 있는데,
    그중 하나가 바로 '가중치'라는 수 하나를 부여하는 것
  • 두 정점간의 거리, 이동시간, 두 물건 사이의 교환비율,
    한 정점에서 다른 정점으로 갔을 때 얻을 수 있는 이득/손해 등


-> 간선에 가중치를 부여해보자!

  • 인접 리스트 adj[s].push_back({e,c}); s에서 e로 가는, 가중치 c를 갖는 간선
    : pair을 이용해서 간선의 가중치도 같이 넣는다. 
  • 인접 행렬 adj[s][e]=c;
    : 연결을 1로 나타내는 게 아니라 그 가중치로 나타낸다.

 

 

최단경로 알고리즘

BFS를 이용하면 그래프에서의 최단경로를 구할 수 있다.
하지만 BFS는 간선에 가중치가 없는 그래프에서만 사용할 수 있다.

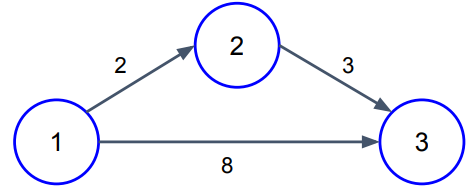
위의 그래프에서 BFS를 이용하여 처음 3번 정점에 도달할 때까지 이동한 거리를 구하면 8이 된다.
하지만 간선에 가중치가 있기 때문에 2번 정점을 거쳐서 가는 길이 거리 5로 더 최단 거리이다.

따라서 가중치가 있는 그래프에서의 최단거리/최단경로를 찾기 위해서는
다른 알고리즘이 필요하다!!

 

 

벨만-포드 알고리즘

  • 한 노드에서 다른 노드까지의 최단 거리를 구하는 알고리즘이다.
  • 간선의 가중치가 음수일 때도 최단 거리를 구할 수 있다.
  • 시작점에서 모든 점까지의 최단거리 dist를 그 상한(INF)으로 초기화해놓고 시작한다.
    이때, 시작점의 dist[1]=0이다.
  • 모든 정점을 순회하며 dist 값을 최단거리에 가깝게 갱신해나간다.
    : dist[next] > dist[cur] + d(cur, next) 라면 dist[next] = dist[cur] + d(cur, next) 으로 갱신해준다.
     이때, dist[cur]!=INF (cur정점이 이미 한번 방문해서 최단거리를 갱신했음)일 때만 갱신해준다. 
  • 모든 정점을 순회하며 최단거리 배열을 갱신하는 위의 과정을 (정점개수)-1 번 만큼 반복한다.
    : A점에서 B점까지의 최단 경로는
     아무리 길어도 A점을 제외한 모든 정점을 한 번씩 지난 후 B점으로 도달하는 경로이다.
     모든 정점을 순회하면서 최단 거리 배열을 갱신하는 작업을 k번 했다고 했을 때,
     k개 이하의 간선들을 사용하는 최단경로는 다 찾을 수 있다.
     따라서 최단거리 배열의 갱신 횟수는 (정점개수)-1 번이면 충분하다.

출처: https://www.acmicpc.net/board/view/74846

 

  • 음의 사이클 문제
    : 사이클의 가중치 합이 음수인 사이클이 있다면 그 경로의 가중치 합이 무한히 작아질 수 있으므로
     최단경로를 제대로 정의할 수 없다.
     따라서 그래프에 음의 사이클이 존재하는지 판정할 필요가 있다.

    음의 사이클이 없으면 V-1번의 갱신으로 시작점에서부터 다른 모든 정점까지의 최단거리를 찾을 수 있다.
    하지만 음의 사이클이 존재한다면, V번째 갱신을 시도했을 때 최단거리가 갱신되는 정점이 있다.
    따라서 V번째 갱신 시도 시 최단거리 갱신되는 정점이 있으면 음의 사이클이 존재한다는 것을 알 수 있다.
     
int bellman_ford(int st, int ed){
    fill(dist, dist+MAX_V, INT_MAX);
    dist[st]=0;
    for(int iter=1; iter<=n; iter++){
        //모든 간선 확인작업을 n번 반복
        for(int cur=1; cur<=n; cur++){
            if(dist[cur]==INT_MAX) continue; //아직 이어지지 않은 정점은 패스
            for(auto &u:adj[cur]){
                int next=u.first, cost=u.second;
                if(dist[next]>dist[cur]+cost){
                    dist[next]=dist[cur]+cost;
                    if(iter==n) negative_cycle=1; //n번째 순회에서 갱신되면 음의 사이클 존재
                }
            }
        }
    }
    return dist[ed];
}

 

  • 시간 복잡도
    가장 바깥 for문은 V번 수행되고 내부 for문은 모든 간선을 순회하므로 E번 수행된다.
    따라서 벨만 포드 알고리즘의 전체 시간 복잡도는 O(VE)이다.

 

*참고자료 
: 벨만 포드 개념 1, 개념 2, 정점 개수만큼 반복 이유

 

 

다익스트라 알고리즘

  • 한 노드에서 다른 노드까지의 최단 거리를 구하는 알고리즘이다.
  • 간선의 가중치가 모두 음수가 아닐 때만 작동하는, 벨만 포드보다 더 빠른 알고리즘!
  • 시작점에서 가까운 순서대로 정점을 방문한다.
    현재 시점에서 시작점에서 가장 가까운 (최단거리가 짧은) 정점을 찾기 위해 우선순위 큐를 사용한다.
  • 정점을 방문할 때마다 인접한 정점을 모두 검사하며 최단거리를 갱신한다.
    : 주의사항! 우선순위 큐에 이미 들어있는 정점의 최단경로가 갱신될 수 있다.
     큐에서 변경 연산은 불가능하므로 그냥 새로운 원소를 추가한다. min-heap이라 작은 값이 먼저 나오니까 노상관
     만약 visited[cur]이면 이미 그거보다 더 작은 값으로 처리했다는 뜻이므로 pop()하고 무시해주면 된다. 

 

int dijkstra(int st, int ed){
    int dist[MAX_V], prev[MAX_V];
    fill(dist, dist+MAX_V, INT_MAX);
    fill(prev, prev+MAX_V, -1);
    int visited[MAX_V] = {0};
    priority_queue<pair<int,int>, vector<pair<int,int>>, greater<>> pq; //min heap {dist, 정점}

    dist[st]=0;
    pq.push({0,st});
    while(!pq.empty()){
        int cur=pq.top().second; pq.pop();
        if(visited[cur]) continue; //이미 방문한 곳이면 무시
        visited[cur]=1;
        for(auto &k:adj[cur]){
            int next=k.first, cost=k.second;
            int next_dist = dist[cur]+cost;
            if(dist[next]>next_dist){
                //최단거리 갱신
                dist[next]=next_dist;
                prev[next]=cur; //최단경로 구하기
                pq.push({dist[next], next});
                // max-heap인 pq에 pq.push({-1*dist[next], next}); 해도 됨
            }
        }
    }
    return dist[ed];
}

priority_queue에 비교 함수를 정의해서 min-heap으로 만들어도 되지만,
최단거리를 음수로 만들어서 넣어줌으로써 max-heap을 min-heap으로 사용해도 된다.

  • 최단 경로 구하기
    prev배열을 이용해서 최단 경로상에서 이전에 지났던 정점을 저장해놓는다.
    그러면 목표 정점에서 역추적해나가면서 시작점까지의 최단 경로를 재구성할 수 있다.
        vector<int> ans;
    int idx=m-1;
    while(idx>=0){
        ans.push_back(idx);
        idx=prev[idx];
    }
    reverse(ans.begin(), ans.end());
    for(auto &k:ans) cout<<k<<" ";

 

  • 시간 복잡도
    우선순위 큐를 이용해서 방문하지 않은 정점 중 시작점에서 가장 가까운 정점을 뽑아
    인접한 정점들의 최단거리를 업데이트하는 과정은 최대 간선 개수 E만큼 이루어진다.

    방문하지 않은 정점 중 시작점에서 가장 가까운 정점을 뽑는 것은
    우선순위 큐의 특성상 O(logN)이다. (N은 우선순위 큐의 원소 개수)
    우선순위 큐의 최대 원소 개수는 간선 개수와 같고 대개의 경우 그래프에서 간선의 개수 E는 V^2보다 작으므로
    O(logN) = O(logV^2) = O(2logV) = O(logV)이다.

    따라서 다익스트라 알고리즘의 총 시간 복잡도는 O(ElogV)이다.

 

 

 

관련 문제

728x90

'PS > Algorithm' 카테고리의 다른 글

플로이드-와샬  (0) 2022.05.27
[알고리즘 개념정리] 11. 분리집합/최소 신장 트리  (0) 2022.02.17
[알고리즘 개념정리] 9. 트리  (0) 2022.02.09
[알고리즘 개념정리] 8. 그래프/그래프 탐색  (5) 2022.02.05
[알고리즘 개념정리] 7. 이분탐색/분할정복  (0) 2022.02.02

관련글

댓글

티스토리툴바